高尔夫挥杆动力学双摆模型
1. 双摆模型
图1显示了手臂和高尔夫球杆在全挥杆过程中的运动,高尔夫研究人员用来分析这种运动的主要模型基于双摆或叫双连杆系统,此模型中使用的两个链接包括在图1中。上面的连杆代表高尔夫球员的肩膀和手臂,它们围绕球员肩膀之间大致中心位置的轮毂旋转。下面的连杆代表高尔夫球杆,它围绕位于高尔夫球员的手和手腕中心的“铰链“旋转。双摆模型认为球员下杆时保持左臂挺直。这个在模型通常并不考虑上杆过程,两个链接开始于图1(a)所示的上杆最高点处上下杆转换时刻,在这个上下转换过渡瞬间,整体动作一般会保持短暂的静止,角度θ是上杆到顶部时上连杆的角度,我们称之为上杆角;上连杆相对于下连杆角度我们称为屈腕角度α。下杆时,两个连杆在一个倾斜挥杆平面上旋转。在模型的基本版本中,位于两肩之间的轮毂是固定处于适当的位置,高尔夫球员旋转他的臀部、躯干和手臂等运动,相当于有一个力偶τ0,施加于这个旋转系统的中枢轴,且通常假设力偶τ0在整个下杆期间保持不变。
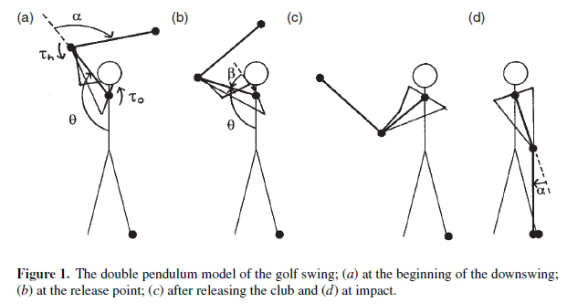
对高尔夫职业球员的手臂和球杆的角度位置的测量发现屈腕角度在下杆的前半段是大致保持不变的,因此,在双摆模型里通常把下杆分成两个阶段。下杆的第一阶段屈腕角度不变,只有一种旋转存在,屈腕角度值主要由球员屈腕能力决定。由手和手腕制造的力偶τh作用于球杆,以维持这个屈腕角度,图 1(a) 所示的方向,最初方向为正,在此期间,这个力偶τh阻止球杆掉向球员。随着下杆的进行,作用在下连杆上的离心力会增加,需要保持屈腕角度的力偶τh量值会减少。当所需的耦合下降到零时,除非我们手腕阻止,否则下连杆将会向外摆动。这被称为自然释放。Jorgensen (1970) 指出,对于基本双摆摆动模型, 当上连杆摆动过IL/2LUSL的一个角度,即图 1(b) 中的β时,所需的手腕力偶下降到零,其中SL和IL是球杆绕球员手中心的一阶矩(质心)和二阶矩(转动惯量),LU是上连杆的长度。 对于典型的挥杆和一号木大约是47°,下杆过程上连杆摆动过这个角度时,上连杆就会向外摆动,图1(b)中的θ称为释放角度。专业的高尔夫球员通常超过这个自然释放点还能够继续保持屈腕角度不变,这时力偶τh方向变负了,力偶的值逐渐增大。典型的下杆持续时间大约200毫秒,模型的第一阶段通常持续100到150毫秒。
下杆的第二阶段开始于球杆向外摆动,要么顺其自然,要么延迟释放,这个阶段结束于与球的碰撞。在这个阶段,通常认为手和手腕力偶τh为0,延迟释放相对于与自然释放,由于作用在球杆上的离心力更大,球杆往外摆动的速度会更大,如图1(d)所示,高尔夫球通常是位于轮毂前面,因此在撞击时最终的屈腕角α不等于零。
Daish (1972)、Lampsa (1975) 和 Jorgensen (1970, 1994) 使用拉格朗日方法推导出基本双摆模型运动方程的表达式,确定两个连杆的动能表达式,并且系统的势能等于轮毂和手上的力偶所做的功。在忽略重力影响的最简单的情况下,Daish (1972)推导出以下运动方程:
![]()
![]()
其中广义坐标φ和θ是两个连杆相对于垂直方向的角位置。上连杆的角度位置θ如图 1(a) 所示,而下连杆的角度位置φ由θ + α给出。常数A、B和C是两个连杆的质量、长度以及一阶和二阶矩的函数。在下杆的第一阶段,屈腕角φ - θ保持固定,一般方程简化为:
![]()
这里I是整个系统对轮毂的转动惯量。
在两阶段双摆模型中,在撞击时球杆的方向将取决于施加在轮毂处的力偶的大小,以及上杆、初始屈腕和释放角度。在图1(d)中,球杆在击球时处于垂直位置,这通常是我们想要的。图2显示了一个示例,其中轮毂力偶的值、释放角度和屈腕角的值与图1中使用的值相同,只是上杆大大减小。在这种情况下,在撞击时手会领先于杆头,将会打不着球或误打误撞。但如果再增加上杆角度,在其他参数固定的情况下,模型显示杆头在撞击球时会领先双手。因此,在这个模型中时序是至关重要,因为它与真实的高尔夫挥杆一样,如果想使杆头击球扎实,改变模型中的一个参数则其它参数也一定需要改变。
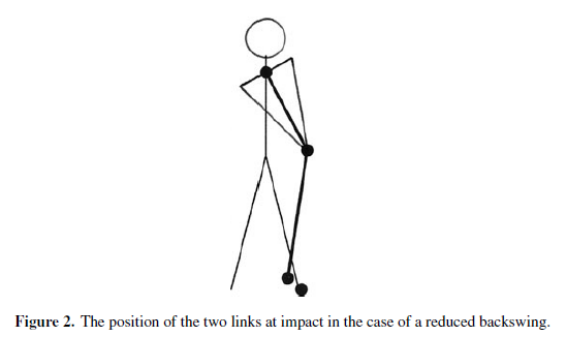
尽管两阶段双摆模型很好地近似于熟练高尔夫球员的下杆,但研究人员发现,如果去除固定轮毂的约束,理论和实际可以获得更好的一致性。Jorgensen(1994)对一名职业高尔夫球员的挥杆进行了详细研究,结果表面:考虑包括轮毂的横向移动是必要的,这么做使得球杆的位置和等数据在模型和实际之间都能具有良好的一致性,这一点可以通过下杆时的高速摄像来验证。通常建议高尔夫球员在挥杆期间保持他们的核心(或轮毂)稳定,但职业选手的高速录像表明他们通常在下杆期间确实向球的方向做了横移。Jorgensen根据这种情况,使轮毂开始加速向球的方向移动然后减速。图3显示了由Jorgensen的摆动模型确定的两个连杆的位置。轮毂扭矩为恒定的77.3Nm,以及166°上杆角、124°的初始屈腕角和大约110°的释放角用于产生这种下杆。在下杆的前160毫秒内,轮毂的横向加速度为14.4ms-2 (1.47g),随后是15.4ms-2 (1.57g) 的负加速度。Jorgensen的双挥杆模型中使用的参数不能被认为是唯一的,尽管模型计算出的杆头速度与测量到的实际速度之间获得了非常好的一致性。

Jorgensen (1994)还讨论了模型化下杆过程中的能量转移。双摆系统的轮毂力偶τ0(假定为常数)在下杆期间所做的功为τ0 × β。在Jorgensen的模型中,还通过轮毂的横向移动和重力对系统做功。图4显示了摆动模型中两个连杆的动能随时间演变的结果。如图所示,上连杆的动能首先增加,在挥杆的中途达到最大值,然后减少。在整个下杆过程中,下连杆(球杆)的动能总是增加。该图清楚地表明,在下杆过程中,动能从上连杆传递到下连杆,手在撞击前的减速行为是自然行为,虽然一些高尔夫专家建议避免这么做。对于这个特定的摆动模型,系统在撞击时的总动能的71%来自施加在轮毂处的力偶所做的功,13% 来自重力能量的减少,16%来自在撞击时轮毂向目标移动所做的功。

Reyes和Mittendorf (1999)使用Jorgensen横向移动的一种变体模型来模拟一号木的挥杆。在这个模型中,横向移动是由于在下杆期间施加在轮毂上的恒定力。他们发现,在轮毂上施加40.0N的横向力和81.3Nm的轮毂力偶时,他们的模型与Jorgensen的模型匹配得非常好。他们还发现,在模拟一号木时,为了使撞击时的模型计算出的和实测的杆头速度,需要一个94.9Nm的轮毂力偶,89.0 N的横向移动力,以及 180°的上杆角和90°的初始屈腕角。
Miura (2001) 提出了一个双摆挥杆模型,其中在撞击前在轮毂处施加向上的力。在一些专业球员挥杆时已经观察到了撞击阶段的这种向内拉动。Miura发现,在撞击前的最后 40 毫秒内,对模型施加的轮毂持续向上的加速度导致低差点高尔夫球员的手部位置得数据在模型和实测之间具有很好的一致性。
Lampsa (1975) 没有使用标准的两阶段下杆模型,而是使用最优控制理论来确定在下杆过程中τ0和τh应该如何变化,以使杆头速度在击球时达到最大值,这些力偶的峰值和下杆的总时间在分析中都是固定的。最优τ0和τh都被发现在下杆过程中近似线性增加。分析的一个有趣结果是,不仅发现杆头速度以与标准的具有常数τ0的两阶段模型基本相同的方式演变,而且发现计算出的屈腕角度保持大致恒定在下杆的前半段。这意味着在轮毂和手部施加平稳增加的扭矩可以在下杆的初始部分给出相同的明显恒定的屈腕角度,这是在职业高尔夫球员挥杆时观察到的,并且内置于两个阶段的双摆模型中。
2. 增加杆头速度
研究人员使用双摆模型来确定各种挥杆参数对杆头冲击速度的影响。击球时的杆头速度是决定击球距离的主要因素,作为粗略的近似,杆头速度每增加一个百分比,就会导致击球距离相应增加一个百分比。然而,在改变挥杆模型中的参数时,如果要与实现扎实击球,则高尔夫球杆在击球时需要大致垂直。这通常意味着如果一个参数发生变化,则需要更改另一个参数以保持正确的时序。
正如预期的那样,增加双摆模型中的上杆角或初始屈腕角度会导致更大的击球时杆头速度。例如,Reyes和Mittendorf (1999) 发现,对于他们的挥杆模型,将上杆角度从180°增加到190°,增加5.6%,导致杆头速度增加约3.1%。然而,该模型也表明(Mittendorf 和 Reyes 1997)改变上杆角度或初始屈腕角度对动作时序有显着影响。例如,在保持其他挥杆参数不变的情况下增加上杆角度通常会导致杆头在击球时领先高尔夫球员的手,而增加初始屈腕角度导致双手领先球杆。
释放角度是挥杆参数之一,它对杆头速度的影响并不明显。如前所述,测量结果表明,专业的高尔夫球员通常会保持最初的屈腕角度超过自然释放点。Cochran和Stobbs (1968)、Jorgensen (1970, 1994)以及Pickering和Vickers (1999)都在双摆摆动模型中考虑了延迟释放球杆的影响,并发现,一般来说,这将导致以更大的杆头速度击球。例如,Pickering和Vickers 发现,对于他们的挥杆模型,将释放角度从132°(对应于自然释放)降低到90°,导致击球时杆头速度增加约3%。延迟释放球杆通过在下杆过程中使球杆更靠近轮毂来提高击球时的杆头速度,从而减少双摆系统围绕轮毂的一阶和二阶矩。然而,延迟释放也会对击球时球杆的方向产生影响,一般来说,手在击球时应该领先杆头。
Pickering和Vickers (1999)还研究了将高尔夫球定位在轮毂点前方的效果。这是高尔夫球员的通常做法,包括在图1(a)中。这样做的一个好处是,对于一个适当的挥杆时间,杆头速度将在整个下杆过程中增加。因此,将球向前定位并因此延迟击球将导致更大的杆头击球速度。Pickering和Vickers在他们的挥杆模型中专门确定了在击球时会导致杆头速度的最大水平分量的球位置。他们发现,在开球和自然释放的情况下,最佳球位置是轮毂位置前方 0.226m,这个位置与将球放置在与轮毂对齐的位置相比,会使杆头速度增加了1.3%。对于延迟释放,效果会稍大一些。例如,在110°的释放角度,他们发现最佳的球位置是轮毂前部0.249m,相应的击球时杆头速度增加了1.6%。皮克林(1998)也考虑了其他球杆的最佳球位置,并发现对于更短和更大杆面高度的球杆,球应放置在更靠近轮毂位置的位置,以最大限度地提高撞击时杆头速度的水平分量。
当然,增加轮毂力偶也将有望提高杆头击球速度。Jorgensen (1994)发现,在他的挥杆模型中,τ0增加5%,导致击球时杆头速度增加1.7%。Reyes和Mittendorf (1999) 发现,在他们的挥杆模型中,τ0增加29%会导致杆头速度增加8.5%。因此,杆头速度的增加与在轮毂处施加的力偶的增加不成比例。不仅轮毂力偶的大小会影响击球时的杆头速度,还会影响轮毂在下杆过程中的演变方式。正如已经讨论过的,Lampsa (1975) 发现,就最大化杆头速度而言,最佳的轮毂力偶是在整个下杆过程中近似线性增加。
Jorgensen (1994) 还考虑了在整个下杆过程中对手和手腕施加正向力偶的影响,此外还考虑了在第一阶段保持恒定屈腕角度所需的力偶。 令人惊讶地发现,对于给定的挥杆模型,额外的正力偶导致击球时的杆头具有较低的速度,因为球杆过早地被带回。当然,在手部应用任何额外的正力偶的效果将取决于特定的挥杆模型。例如,在延迟释放后在手部应用正向力偶合不仅可以提高杆头速度,而且可以使时序正确。
正如已经讨论过的,Jorgensen (1994)和Miura (2001)发现为了在双摆模型和实验测量之间获得良好的一致性,必须去除固定轮毂的约束。Jorgensen考虑了轮毂的不同横向移动或不同加速度对杆头撞击速度的影响。从模型中完全去除横向偏移导致击球时的杆头速度降低了大约8.8%。增加横向移动导致击球时的杆头速度提高了17%。当然,任何横向移动都需要与双摆系统的运动同步,以实现杆头速度的这些改进,以及保持球杆在击球时的方向。 Miura发现,在他的挥杆模型中,在击球前的最后40毫秒内,包括轮毂的向上移动,导致击球时的杆头速度增加了大约7%。